Now, with the US Open tennis championship starting this week and already in full swing, I thought we tackle something that have been a small puzzle for me. Maybe someone has a good explanation for it.
The one thing they also do in many of these tennis tournaments, especially the bigger ones, is to also monitor the speed of the serves. Venus Williams, for example, is cited to have the current fastest serve in women's tennis, at 129 miles per hour, I think. So naturally, my curiosity wonders on how they determine that. Unlike baseball, if they use the same type of radar gun, there is a possibility that they may not get an accurate reading of the speed of the ball. Here's why:
The layout below is a standard tennis court with all the dimensions.
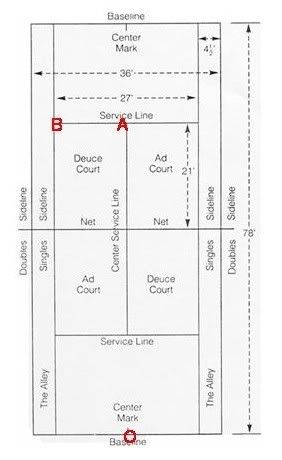
Now, let's say the radar gun is placed directly in line with the center line of the court (i.e. in line with OA). Now, already you can tell that such device will only give the most accurate reading if the ball is coming towards it, i.e. moving along OA. If the ball is moving at an angle to OA, it won't give an accurate reading.
I did a quick calculation on how much the reading would be different. For simplicity sake, we have a person standing at O, hits a serve that lands at B. Let's say the ball travels at v_OB = 130 mph. For a radar gun that is placed directly along the OA line, it will measure only that component of the velocity v_OA, i.e. the component moving in the direction of OA. The angle AOB is ~13 degrees. Thus
v_OA = v_OB * cos(13).
In this case, with v_OB = 130 mph, we get v_OA = 126 mph This means that the radar gun will only read 126 mph, 4 mph less than the actual speed of the ball. Does that mean that Venus Williams actually served faster than 130 mph when she hit that serve? And this is only a more conservative scenario where I placed the server at O. In practice, the server can be at an even more severe angle and serving even wider off the court, meaning that the angle we are dealing with is larger than 13 degrees. This makes the reading of the speed even more inaccurate.
Now, the only caveat here is that I'm assuming that they're using this "antiquated" technique in determining the speed of the ball. With the use of Hawk-Eye system that is in place at all the 4 major tournaments (and others), that system could be the one being used to determine the speed of the ball. In that case, the actual trajectory of the ball isn't determined by just one radar gun placed along the center line. So the actual reading of the speed is more accurate that what I've described. Still, I don't know if they use Hawk-Eye to determine the speed of the serve, and I think that for many tennis tournaments, especially the ones without Hawk-Eye, they might still be using a radar gun.
The consolation here is that the determination of the speed of the serve is irrelevant in the playing of the game. It's nice to have a fast serve, but knowing how fast it is doesn't enter into the game at all. So maybe that's why not much effort is put into making such an accurate determination of the speed of the serve.
Zz.
2 comments:
I'm also a little curious whether the speed they list is the instantaneous speed at the racket, the instantaneous speed at the net, the receiver, the landing point, or if it's an average speed, over any of a number of possible choices od time-frames (OK, it must be averaged over a millisecond, say, instantaneous is not possible). Again, the Hawkeye system presumably models the speed as continuous, so it could give a multitude of answers. Mathematicians should unite in a call for thorough graphical presentations! There might perhaps be a teaching aid in there.
I've always believed it to be measured over the first 3 feet - possible a metre these days.
Post a Comment