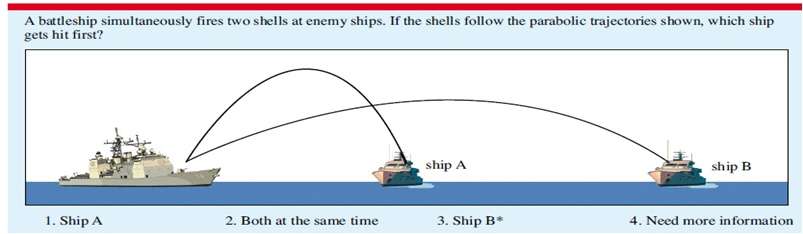
I was reading the July 2010 issue of Physics Education, one of IoP journals, and came across this rather interesting, seemingly-simple projectile motion problem. Supposedly, this was taken out of Eric Mazur's "Peer Instruction" book. I will post the figure here:
The question is rather simple based on that figure. If the battleship simultaneously fires two shells at enemy ships and follow the shown parabolic trajectories, which ship gets hit first?
The question gives 4 possible answers: (1) Ship A, (2) Both at the same time, (3) Ship B, and (4) Need more information.
The level of physics needed to solve this is first year undergraduate intro physics, or even AP physics. It is how you approach the problem to solve this that may require a little bit of sophistication. See if you can find the answer, and I'll post mine in another blog post later... :)
Zz.
17 comments:
Are we supposed to take into account air resistance? Because this seems fairly physically intuitive otherwise.
Isn't this the same as tossing two balls vertically with different speeds and asking which comes down first? I.e. the shell w/ lower vertical velocity (Shell B) lands first.
Also I think you mean "enemy ships" instead of "energy ships".
Note that it clearly stated parabolic trajectory. That should tell you what kind of assumptions you can make.
I'm not sure if it is the same as tossing two balls, because here, the position or range of the two objects are not the same. Also, one presumes that the initial velocity of the projectile is the same, since they came from the same ship.
I've corrected my typo. Thanks.
Zz.
So if we represent the velocities as vectors:
v_a(t) = v* - <0, gt>
v_b(t) = v* - <0, gt>
We know that there's really only one degree of freedom in the system (θ), so there's a one-to-one map from firing angles to hit positions, right? In other words, when the shell gets back to ship-level it is guaranteed to be at its final x-position.
Thus we need only to solve in one dimension; because the distances are not specified this is easier to do in the y-axis. (This is where my simplification to ball-tossing comes in.) Because of conservation of energy, when the shell hits the ship, the vertical speed will the same (but in the opposite direction). Clearly, with constant acceleration, the ball that starts with the lowest vertical velocity, or lowest firing angle, will flip its vertical velocity—and thus reach its target—first.
Yes, I think Theo is right. Assuming the speeds of the shells are the same and disregarding air resistance, I think the problem can be reduced to the balls example. Here's why.
We can consider the parabolic trajectory as its two components, vertical and horizontal. The speed of each component depends on the angle, which can give you the time it takes to do complete its vertical or horizontal trajectory. Since each shell hits its target, we can tell that the vertical and the horizontal times are the same (otherwise it would hit before or after the ship).
Knowing that, we can ignore the horizontal component and consider only the vertical component, which reduces the problem to the balls example.
And, as concluded by Theo, the Shell B has lower vertical speed so it takes less time to get slowed down to 0 going up and back to initial speed going down, when it hits Ship B.
Just correcting myself, I think the times of the components are always the same, hitting or missing the ship.
In any case, that doesn't change the conclusion.
Theo: Oh, now I see what you're getting at. I didn't quite understand your original description.
Zz.
yeah. the further ship gets hit first.
the motion is parabolic, which implies no air resistance.
the vertical motion will determine the time of flight. since the closer ship's shell goes higher in the vertical direction, it's time of flight is longer.
I'll go with need more information. Let's assume the initial velocity is 1. The trajectory is [cos(angle) t, sin(angle) t - g t^2/2]. The vertical component is 0 at time t0 = 2 sin(angle)/g and the horizontal distance is sin(2 angle)/g. So either we need to assume angle < 45deg in which case the closer ship gets hit first, or angle > 45deg in which case the farther ship gets hit first.
I believe that the ship farthest away gets hit first. Here's why:
Neglecting air resistance, from 1-d kinematics in the y-direction the total time required to complete a parabolic trajectory for a given theta (as measured from the horizontal) and initial velocity Vo is:
T = 2*Vo*sin(theta)/g
Considering two different trajectories (theta1, theta2) with identical initial velocities Vo:
T1 = 2*Vo*sin(theta1)/g
T2 = 2*Vo*sin(theta2)/g
Dividing the two equations gives:
T1 = T2 sin(theta1)/sin(theta2)
The condition that theta1 < theta2 implies that T1 < T2. Thus, the farthest ship gets hit first.
The farther one will get hit first, because the parabola for this ship is lower, implying less time for its vertical motion.
Looks like id need more info. Am I to assume that these three points make a straight line? In other words, the boats can be the same distance away from the boat with the same trajectory, but since you're only seeing them in one dimension they only seem to be different.
My issue with this problem is that it paints a picture of a stupid gunner on the ship, or perhaps of a problem writer who creates physics problems that are distant from reality. Why fire the high lob shot at the closer ship? I don't think that is what artillery gunners are taught in artillery school.
You're missing the point.
We teach students Newton's Laws using projectile motion and inclined planes NOT because we want to teach them about shooting canons or sliding down the hill. The examples have nothing to do with what they should learn. Instead, they are illustrations on how such laws are APPLIED. Without applying these physics concepts into specific situations, one only learn such concept superficially.
So it really has nothing to do with shooting canons. It has everything to do with understanding and realizing how forces and motion in orthogonal directions can be "decoupled", with only the time of the motion connecting those two directions.
Zz.
We disagree, Zapper. I understand the problem. I have taught introductory physics at the college level. It's hard to make those students understand what seems so obvious to me.
I don't think that this problem has great didactic value. I can't help thinking that your average physics 101 student will get it wrong. I'm not familiar with Mazur's book. Perhaps he is a great physics teacher, and a lousy artillery instructor. If only he were available for comment. …
Again, you're missing the point here.
In Mazur's book, this is NOT a HW question. It is more of an assignment in which students discuss among themselves to arrive at an answer, thus the name "Peer Instruction"!
I see great value in something like this. This is no different than a discussion of finding out which cylindrical can will roll down an inclined plane first if they have identical weight, but one is hollow in the middle.
I posted this question outside my door at work. Even other physicists and graduate students stopped by and expressed a curious interest in the question.
Zz.
So... as a physics student... I want to know what is the correct answer? I also think that the one with less height will arrive first... but how is right?
The answer seems rather simple assuming normal projectile conditions.The time of flight is only dependent on height of trajectory and 'g'.now since 'g' is constant the farther ship must be hit first.
Post a Comment