How Quickly Does A Photon Reach c?

I've seen this question numerous times. The premise here is that while a photon travels at c in vacuum, it wasn't "born" with that speed. Somehow, after a photon is created at some low speed (zero?), it then accelerates to c. So I often get asked on how quickly does it reach c.

There are several problems with such a question, and this certainly qualifies as a "When did you stop beating your wife?"-type of question. Why? Because it assumes, a priori, that photons CAN have speeds other than c in vacuum. This is not verified. So the idea that a photon gets born with some low speeds is not an idea that has any physical basis, and thus, the starting point is all wrong.

Secondly, there is a problem in reconciling our experimental evidence with such a scenario. Let's look at this carefully.

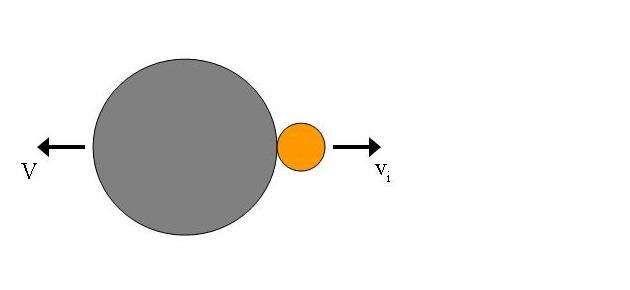
Say we have a body that is initially at rest. at some point, emits a particle, as shown in the figure below.

The larger body moves with velocity V, while the smaller body moves with velocity v_i. These two values are related to each other via conservation of momentum.

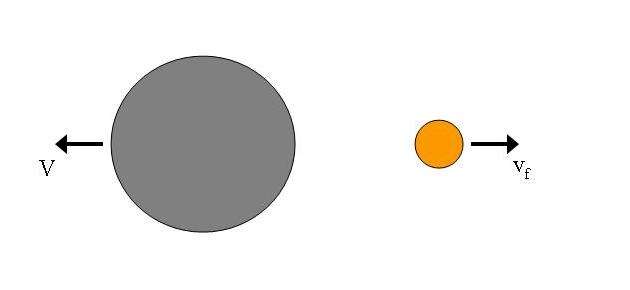
Now, let's say that the smaller body then accelerates, by some means, to some final velocity, as shown below.

 

However, this final velocity v_f has no directly relations to V, i.e. it isn't correlated to V since the conservation of momentum of the two bodies no longer is relevant here. v_f no longer carries any direct information about V.

So let's look at what we know about such a thing. Atomic recoil, electron recoil, and a while bunch of other experiments on photo emission and photon collision experiments have shown that what we measure in such interactions totally conserve momentum. In other words, we measure v_f (since it was already at c for photon), and this v_f is still correlated to V via a direct conservation of momentum. This clearly means that v_f is equal to v_i, and therefore, there is no "acceleration" of photons

This scenario applies to a whole zoo of fundamental particles as well since the same conservation law applies to many  such interactions involving these particles.

Zz.